En el post anterior pintamos un cuadrado de color rojo. Recordamos que era tan sencillo como escribir en el fragment shader la línea

return float4(1.0, 0.0, 0.0, 1.0); 

Pero, ¿y si queremos pintar el mismo cuadrado de varios colores? En particular, ¿cómo podríamos hacer un gradiente de color, de un vértice del cuadrado a su opuesto?

Información de los vértices

Los vértices de una malla pueden tener más información, además de la evidente, su posición. Entre otros atributos tenemos el color del vértice. Si por ejemplo, queremos asignar un color a cada vértice de un quad, bastaría añadir el siguiente script a este objeto

    public Color[] colors;

    void Start () {
        Mesh m = GetComponent<MeshFilter>().mesh;
        m.colors = colors;
    }

donde el array de colores lo definimos en el inspector de Unity.

Esta información que definimos en cada vértice puede recogerse en el shader y usarse para colorear la malla. Un shader que hace uso de esto sería el siguiente

Shader "Morvaly/VertexColorShader" {
    SubShader {
        Pass {
            CGPROGRAM

            #pragma vertex vert
            #pragma fragment frag

            struct appdata {
                float4 vertex : POSITION;
                float4 color : COLOR0;
            };

            struct v2f {
                float4 pos : SV_POSITION;
                float4 col : COLOR0;
            };

            v2f vert (appdata v) {
                v2f o;
                o.pos = mul( UNITY_MATRIX_MVP, v.vertex );
                o.col = v.color;
                return o;
            }

            float4 frag(v2f i) : COLOR {
                return i.col;
            }

            ENDCG
        }
    }
}

Vemos dos elementos que no habíamos introducido hasta ahora: las estructuras struct.

Estas estructuras sirven como inputs del vertex shader y del fragment shader. En este caso, lo que llega al vertex shader desde C# es la estructura appdata que contiene los atributos vertex y color, definidos en la malla.

Por otro lado, el vertex shader tiene como output otra estructura v2f, que sirve como input para el fragment shader.

De los vértices a los fragmentos

El vertex shader se ejecuta una vez por vértice de la malla, devolviendo la estructura v2f. Por otro lado el fragment shader tiene como input una estructura del tipo v2f.

Esto parece un poco raro, ya que el fragment shader se ejecuta una vez por pixel, en el triángulo definido por tres vértices de la malla (no triángulos cualesquiera: triángulos de la triangulación de la malla). Entonces, ¿que valor v2f tomamos para cada pixel?

La respuesta es: la interpolación lineal entre los tres v2f. Es decir, cuando hemos definido el fragment shader como

float4 frag(v2f i) : COLOR {
    return i.col;
}

el input v2f i se refiere a la estructura interpolada para ese pixel.

Esto mola. Mola porque para hacer el gradiente que comentábamos al principio basta fijar un color por vértice y dejar que el fragment shader se ocupe del resto, ya que interpolará los colores.

Haciendo esto, se tiene en Unity lo siguiente

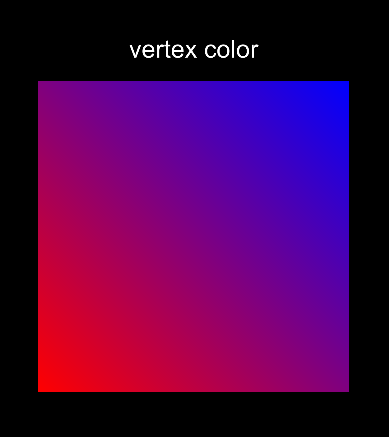
Sencillamente hemos asignado un color a cada vértice, hemos asignado el shader anterior al material del quad y el resto se lo hemos dejado a la tarjeta gráfica.

Esta manera de hacer un gradiente tiene un problema, y es que hemos necesitado cuatro colores (tres distintos) para determinarlo, y en principio, solo se necesitan dos.

Vamos a ver otra manera de hacer este mismo gradiente

Shader "Morvaly/FragmentColorShader" {
    SubShader {
        Pass {
            CGPROGRAM

            #pragma vertex vert
            #pragma fragment frag

            struct appdata {
                float4 vertex : POSITION;
                float4 texcoord : TEXCOORD0;
            };

            struct v2f {
                float4 pos : SV_POSITION;
                float4 uv : TEXCOORD0;
            };

            v2f vert (appdata v) {
                v2f o;
                o.pos = mul( UNITY_MATRIX_MVP, v.vertex );
                o.uv = float4( v.texcoord.xy, 0, 0 );
                return o;
            }

            float4 frag(v2f i) : COLOR {

                float4 red = float4(1.0,0.0,0.0,1.0);
                float4 blue = float4(0.0,0.0,1.0,1.0);

                float u = i.uv.x;
                float v = i.uv.y;

                return lerp(red,blue,0.5*(u+v));
            }

            ENDCG
        }
    }
}

En este shader hemos introducido un nuevo atributo de entrada para el vertex shader texcoord, de tipo TEXCOORD0. Esta atributo contiene el mapa de coordenadas de la malla, lo que se resume en un par de números (a,b) en el intervalo (0,1) para cada vértice, elegidos de manera coherente.

Esta mapa de coordenadas es fundamental en la texturización de una malla.

En nuestro caso, este mapa de coordenadas es tan sencillo como lo que se representa en la siguiente imagen

Es decir, cuatro valores, uno por vértice...

Para el resto del triángulo entra de nuevo en acción el fragment shader. Basta añadir a la estructura que se le pasa al fragment shader el atributo uv y la línea o.uv = float4( v.texcoord.xy, 0, 0 ); al vertex shader y listo.

Si analizamos con detenimiento el fragment shader, y lo comparamos con el del primer ejemplo, vemos algo que cabe remarcar: este tiene bastante más lógica.

float4 frag(v2f i) : COLOR {

float4 red = float4(1.0,0.0,0.0,1.0);
float4 blue = float4(0.0,0.0,1.0,1.0);

float u = i.uv.x;
float v = i.uv.y;

return lerp(red,blue,0.5*(u+v));
}

Por un lado definimos dos colores, red y blue, y por otro usamos dos variables, u y v, para los valores del mapa de coordenadas. Por último calculamos el color que tendrá el pixel del triángulo, interpolando entre los dos colores definidos, en base al mapa de coordenadas.

Es decir, hemos replicado el funcionamiento de nuestro primer shader.